（これまでの 小島寛之の「環境と経済と幸福の関係」は こちら）

今回は、経済学で「不平等度」を計測するために導入された「ジニ係数」を使った興味深い分析を紹介しようと思う。

「格差社会」というのが話題になってから、「ニート」とか「下流」とかを中心に据えて、世代間格差や正社員・パート間格差などについての論評がたくさん出版され、いくつかはベストセラーになっている。でも、「本当に日本が不平等社会になっているかどうか」、という点については、経済学者の間で論争になっている状態で、まだそんなに明白なことじゃない。なのにマスコミが、ごく一部の特殊な若者の生活ぶりをさも典型的な若者像のように放映するものだから、国民が錯覚に陥っているんだろうな、と個人的には感じている。

今回話すのは、不平等性を評価する「ジニ係数」のことだが、残念ながら、話題の中心は「格差社会」のことではないので、そういう期待をしないで読んでほしい。

不平等の度合いを計測する指標はいろいろあるけど、経済学では「ジニ係数」というのが最もポピュラーだ。ジニ係数の原理は簡単。例えば、測りたいのが「所得の不平等性」なら、まず、国民一人一人の所得額を小さい順に並べる。そして、「下位xパーセントの人の所得の合計が国民所得全体のyパーセントにあたる」とき、座標(x,y)のところに点を打つ。そして、それらを順に折れ線でつなぐ。このようにしてできた折れ線が、「ローレンツ曲線」と呼ばれる。

具体例をやってみよう。今、国民は5人として、100万円を分け合うとする。「完全平等」な分配はいうまでもなく、20万円ずつ分けること。このとき、下位20パーセントの人が20パーセントの所得を、下位40パーセントの人が40パーセントの所得を、という具合になるので、ローレンツ曲線は、当然「対角線」となる。(図中の原点と点(100,100)をつなぐ線)。つまり、「完全平等のローレンツ曲線は対角線」ってことだ。

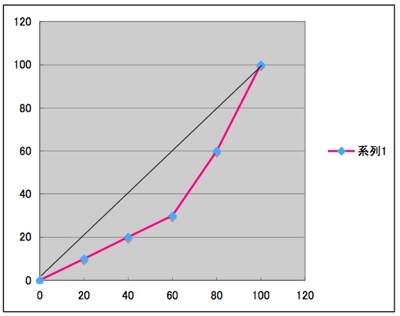
それに対して、100万円の所得を不平等に、10万、10万、10万、30万、40万と分配する場合は、下位20パーセントが10パーセントの所得を、下位40パーセントが20パーセントの所得を、下位60パーセントが30パーセントの所得を、下位80パーセントが60パーセントの所得を、という具合になっているので、座標(20, 10), (40, 20), (60, 30), (80, 60), (100, 100)に打点して折れ線でつないだものがローレンツ曲線になる。図のように、このローレンツ曲線は、対角線よりも右下にむかってたわむ。そして、このたわみ方の激しさが不平等の度合いを表していると考えられる。よって、「ローレンツ曲線と対角線がはさむ領域の面積が、対角線より右下の直角二等辺三角形の面積に占める割合」を「不平等の指標」と定義するのは妥当である。まさにこの「割合」が「ジニ係数」なのである。「完全平等」なときのジニ係数は、当然ゼロ。そして、ローレンツ曲線がたわんで行くにしたがって、対角線とで囲む部分は直角二等辺三角形に近づき、ジニ係数は1.0に近づいていく。つまり、ジニ係数が大きくなって1.0に近づくほど、不平等の度合いが激しくなる、という次第である。

このジニ係数は、導入部で話したように、普通は国民の「所得格差」などの「不平等性」を計測するのに使われる。けれども今回は、それを土地の「価格分布」に応用した面白い発想の論文を紹介したい。それは、海蔵寺&海蔵寺が2004年に発表したものである[*1]。

特記すべきは、これが経済に関する研究論文であるにもかかわらず、物理学のジャーナルに発表された、という点だ。もっと正確に言うと、経済現象を物理の考え方を使って分析する「経済物理学」という非常に新しい分野に属する研究なのである。

海蔵寺&海蔵寺は、日本の1980年代と1990年代の全国の土地価格の分布のジニ係数を計測した[*2]。当時はいうまでもなくバブル期で、土地価格は急上昇していたわけだが、彼らが興味を持ったのは、「土地の平均価格が高いかどうか」ではないのである。彼らが注目したのは、土地価格が全体として「まんべんなく高くなっている」のか、それとも「値上がりが一部に偏っている」のか、そういういう問題だった。そういう「偏り」を計測するには、ジニ係数が適している[*2]。

この論文によれば、ジニ係数は1980〜1984年頃には0.57程度の水準だったものが、1985年頃から急上昇し、1987年〜1992年の間ずっとピーク水準の0.75程度を保っている。そして、この期間にバブルが崩壊を迎えたのは周知の事実である。バブル崩壊後は、急速に下がり2000年には0.5程度の水準に戻っているのである。

このことから、海蔵寺&海蔵寺は、バブルの崩壊は「価格水準がピーク」のときに起きるのではなく、むしろ「価格の偏りがピーク」のときに起きるのではないか、という仮説を提出したのである。

これは、(経済学者である)ぼくがあまり耳にしたことのない仮説であり(単に実証が専門外なための不勉強の可能性も否めないけどね)、物理学ならではの見方からの発見なのでないか、と新鮮に感じられる。そういう意味では、「経済物理学Econophysics」という新興勢力の可能性を示す結果の一つといえるかもしれない。

現在、金融の世界で最もホットな話題は、「アメリカの住宅価格の高騰が、実際はバブルであって、それがはじけたかどうか」、という問題だ。この問題が世界中の金融市場をゆさぶって、世界同時株安を引き起こしている、といわれている。この問題に対しても、ジニ係数の方法論が予言的な結論をもたらすかどうか、誰か研究してくれてるだろうか。とても楽しみである。

＊　＊　＊　＊　＊
[*1] Taisei Kaizoji and Michiyo Kaizoji: A mechanism leading bubbles to crashes: the case of Japan's land markets, Physica A 344 (2004) 138-141.
[*2] 彼らの研究の主たる部分は、
土地価格の累積分布関数(cumulative probability distribution)が、xの(−α)乗という「べき乗則」に従う
という、いわゆる「複雑系」の研究である。ただ、「べき乗則」と「ジニ係数」は、「ジニ係数=1/(2α−1)」という関係で結ばれるらしいので、「ジニ係数」からの分析だと思っても差し支えないのである。

フィードを登録する	経済・ビジネス